

Nächste Seite: Widerstände, Induktivitäten und Reaktanzen
Aufwärts: Die permanentmagnetisch erregte Synchronmaschine
Vorherige Seite: Wicklung
Induzierte Spannung

Die Grundwelle der Luftspaltinduktion induziert die Leerlaufspannung in der
Statorwicklung.
Hierzu muß die Grundwelle der Luftspaltinduktion ermittelt werden.
Aufgrund der radialen Magnetisierung ist die Luftspaltinduktion
rechteckförmig.
Die Amplitude der Grundwelle
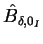 kann über die
Koeffizienten
kann über die
Koeffizienten 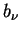 der Fourier-Reihe ermittelt werden.
Die Verteilung der Luftspaltinduktion ist eine ungerade Funktion über
der Fourier-Reihe ermittelt werden.
Die Verteilung der Luftspaltinduktion ist eine ungerade Funktion über 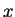 (
(
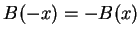 ).
Damit werden die Fourier-Koeffizienten
).
Damit werden die Fourier-Koeffizienten 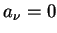 und es müssen lediglich
die Koeffizienten
und es müssen lediglich
die Koeffizienten 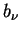 für
für
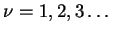 bestimmt werden.
bestimmt werden.
Damit liegt die räumliche Verteilung der Induktionsgrundwelle im
Luftspalt (bei Leerlauf) fest.
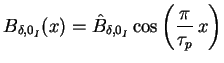 mit mit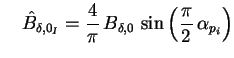 |
(22) |
Der Polformkoeffizient der Grundwelle 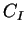 beschreibt das Verhältnis
der Grundwellenamplitude der Luftspaltinduktion
beschreibt das Verhältnis
der Grundwellenamplitude der Luftspaltinduktion
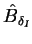 zur der maximalen Luftspaltinduktion über der ideellen Polbreite
zur der maximalen Luftspaltinduktion über der ideellen Polbreite 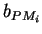 gemäß Abbildung 1.
Bei der hier betrachteten Maschine mit konstantem Luftspalt, d.h. mit magnetisch
rotationssymmetrischem Läufer, ergibt sich:
gemäß Abbildung 1.
Bei der hier betrachteten Maschine mit konstantem Luftspalt, d.h. mit magnetisch
rotationssymmetrischem Läufer, ergibt sich:
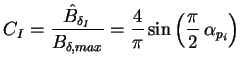 |
(23) |
Die Auswirkungen von Sättigung oder nicht konstantem Luftspalt werden ggf. durch
zusätzliche Koeffizienten berücksichtigt.
Die räumliche Verteilung des Flußes ergibt sich durch Integration der
Induktionsverteilung über eine Polteilung
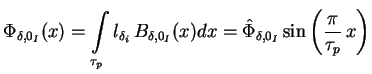 mit mit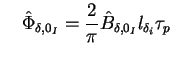 |
(24) |
Aus der Änderung des Flußes ergibt sich die induzierte Spannung 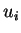 gemäß
Induktionsgesetz aus dem mit der Wicklung verketten Fluß
gemäß
Induktionsgesetz aus dem mit der Wicklung verketten Fluß 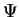
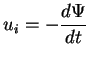 mit mit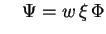 |
(25) |
Bei zeitlicher und räumlicher Änderung, beispielsweise aufgrund einer
Bewegung des Rotors um den Weg 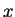 , ergibt sich der
folgende Zusammenhang:
, ergibt sich der
folgende Zusammenhang:
Bei zeitlich konstantem Fluß ergibt sich daraus:
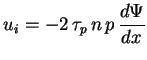 |
(29) |
Die räumliche Verteilung des Grundwellenflußes im Luftspalt einer
permanentmagnetisch erregten Synchronmaschine bei Leerlauf ergibt sich zu:
Aus den Gleichungen (29),
(30) und (31)
ergibt sich für die Grundschwingung der induzierten Spannung im Leerlauf:
Der Effektivwert der induzierten Spannung beträgt somit:
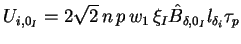 |
(34) |


Nächste Seite: Widerstände, Induktivitäten und Reaktanzen
Aufwärts: Die permanentmagnetisch erregte Synchronmaschine
Vorherige Seite: Wicklung
Sie interessieren sich für die elektrische Antriebstechnik?
Dann besuchen Sie doch auch einmal meine
geschäftliche Homepage.
Volker Bosch
2015-05-27
![]() kann über die
Koeffizienten
kann über die
Koeffizienten ![]() der Fourier-Reihe ermittelt werden.
Die Verteilung der Luftspaltinduktion ist eine ungerade Funktion über
der Fourier-Reihe ermittelt werden.
Die Verteilung der Luftspaltinduktion ist eine ungerade Funktion über ![]() (
(
![]() ).
Damit werden die Fourier-Koeffizienten
).
Damit werden die Fourier-Koeffizienten ![]() und es müssen lediglich
die Koeffizienten
und es müssen lediglich
die Koeffizienten ![]() für
für
![]() bestimmt werden.
bestimmt werden.
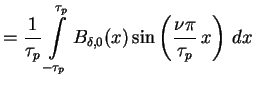 für
für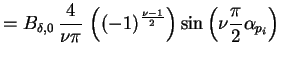 mit
mit![]() beschreibt das Verhältnis
der Grundwellenamplitude der Luftspaltinduktion
beschreibt das Verhältnis
der Grundwellenamplitude der Luftspaltinduktion
![]() zur der maximalen Luftspaltinduktion über der ideellen Polbreite
zur der maximalen Luftspaltinduktion über der ideellen Polbreite ![]() gemäß Abbildung 1.
Bei der hier betrachteten Maschine mit konstantem Luftspalt, d.h. mit magnetisch
rotationssymmetrischem Läufer, ergibt sich:
gemäß Abbildung 1.
Bei der hier betrachteten Maschine mit konstantem Luftspalt, d.h. mit magnetisch
rotationssymmetrischem Läufer, ergibt sich: