

Nächste Seite: Induzierte Spannung
Aufwärts: Die permanentmagnetisch erregte Synchronmaschine
Vorherige Seite: Permanentmagnet und Luftspaltfluß

Die Lochzahl 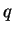 bezeichnet die Anzahl der Nuten pro Pol und Strang.
bezeichnet die Anzahl der Nuten pro Pol und Strang.
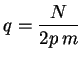 |
(16) |
Der elektrische Nutwinkel 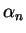 ergibt sich aus Polpaarzahl
ergibt sich aus Polpaarzahl 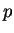 und
Nutzahl
und
Nutzahl 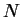 .
.
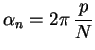 |
(17) |
Für den Wicklungsfaktor ist hier lediglich der Zonenfaktor relevant.
Bei der Einschichtwicklung erhält man den folgenden Ausdruck
für die 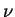 -te Harmonische:
-te Harmonische:
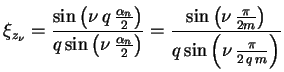 |
(18) |
Die einseitige Wicklungskopflänge 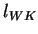 wird aus dem
Bohrungsdurchmesser
wird aus dem
Bohrungsdurchmesser 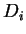 ,
der Nutschlitzhöhe
,
der Nutschlitzhöhe 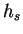 und der Nuthöhe
und der Nuthöhe 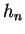 abgeschätzt.
Die Ausladung des Wickelkopfes wird durch die Summe aus maximaler Nutbreite
und maximaler Zahnbreite abgeschätzt.
abgeschätzt.
Die Ausladung des Wickelkopfes wird durch die Summe aus maximaler Nutbreite
und maximaler Zahnbreite abgeschätzt.
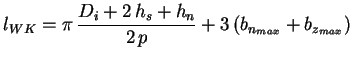 |
(19) |
Die mittlere Windungslänge  setzt sich aus Wicklungskopflänge
setzt sich aus Wicklungskopflänge 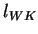 und Statorlänge
und Statorlänge 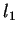 zusammen.
zusammen.
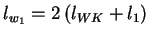 |
(20) |


Nächste Seite: Induzierte Spannung
Aufwärts: Die permanentmagnetisch erregte Synchronmaschine
Vorherige Seite: Permanentmagnet und Luftspaltfluß
Sie interessieren sich für die elektrische Antriebstechnik?
Dann besuchen Sie doch auch einmal meine
geschäftliche Homepage.
Volker Bosch
2015-05-27
![]() bezeichnet die Anzahl der Nuten pro Pol und Strang.
bezeichnet die Anzahl der Nuten pro Pol und Strang.
![]() -te Harmonische:
-te Harmonische: