Die graphische Ermittlung des Arbeitspunkts eines magnetischen Kreises wird
sehr aufwendig - wenn nicht gar unmöglich - sobald Streuung und
Eisensättigung berücksichtigt werden müssen.
Zur Bestimmung des Arbeitspunkts eines solchen ,,vermaschten`` magnetischen
Kreises bietet es sich an den Kreis als Netzwerk konzentrierter
Ersatzelemente darzustellen [1].
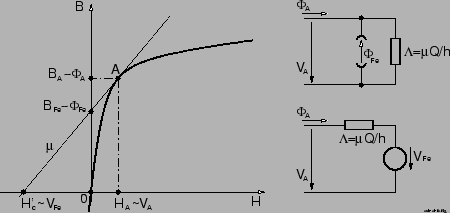 |
Die Durchflutung ![]() entspricht der ,,magnetischen Ersatzspannung``,
der Fluß
entspricht der ,,magnetischen Ersatzspannung``,
der Fluß ![]() dem ,,magnetischen Ersatzstrom``.
dem ,,magnetischen Ersatzstrom``.
Für die numerische Berechnung eines Netzwerks bietet sich die Knotenpotentialanalyse an [3]. Hierfür sind die Netzwerkelemente in Leitwerte und Stromquellen umzurechnen.
 |
Luftspalte und Streuwege in Luft sind lineare Widerstände mit dem
magnetischen Widerstand
![]() , bzw. dem magnetischen Leitwert
, bzw. dem magnetischen Leitwert
![]() .
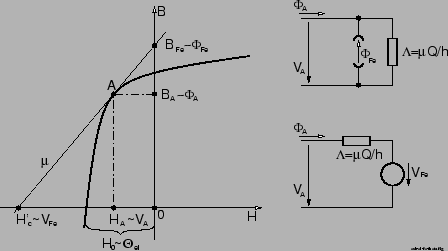
Die weichmagnetischen Jochstücke und die permanentmagnetischen Elemente
werden anhand ihrer Magnetisierungskurve im Arbeitspunkt linearisiert und
durch entsprechende Ersatzstromquellen und Leitwerte ersetzt, wie die
Abbildungen 4 und 6 zeigen.
.
Die weichmagnetischen Jochstücke und die permanentmagnetischen Elemente
werden anhand ihrer Magnetisierungskurve im Arbeitspunkt linearisiert und
durch entsprechende Ersatzstromquellen und Leitwerte ersetzt, wie die
Abbildungen 4 und 6 zeigen.
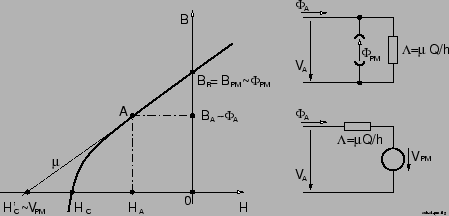 |
Die Durchflutungen (,,magnetischen Ersatzspannungen``) werden anhand der Kennlinien der Ersatzelemente, an denen sie wirken, in entsprechende ,,magnetischen Ersatzspannungsquellen`` umgerechnet. Hierzu müssen die Kennlinien entsprechend der magnetischen Feldstärken verschoben werden. Abbildung 5 zeigt Kennlinie und zugehörige Ersatzquellen eines elektrisch erregten weichmagnetischen Jochstücks.
Die Analyse des Netzwerks erfolgt iterativ, indem die Startwerte für ![]() (magnetischer ,,Kurzschluß``) der einzelnen Elemente bestimmt werden.
Aktive Elemente, also elektrisch erregte Jochstücke und permanentmagnetische
Werkstoffe befinden sich somit im Remanenzpunkt, d.h. der für die
Knotenpotentialanalyse zu verwendende Strom beträgt
(magnetischer ,,Kurzschluß``) der einzelnen Elemente bestimmt werden.
Aktive Elemente, also elektrisch erregte Jochstücke und permanentmagnetische
Werkstoffe befinden sich somit im Remanenzpunkt, d.h. der für die
Knotenpotentialanalyse zu verwendende Strom beträgt ![]() .
.
Es ergeben sich die Potentiale (magnetische Spannungen) der einzelnen Knoten. Die Potentialdifferenz zwischen zwei Knoten entspricht der magnetischen Feldstärke über dem jeweiligen Element. Mit ihrer Hilfe wird für jedes Element der neue Arbeitspunkt (magnetischer Strom und Leitwert) bestimmt. Diese Werte setzt man erneut in die Netzwerkmatrix ein und löst diese.
Für eine sichere Konvergenz dieses Verfahrens kann es notwendig sein, die Magnetisierungskurven von Eisen nur in einem Quadranten darzustellen. Im Ursprung müssen die Kurven (physikalisch falsch) linear fortgesetzt werden. Hystereseeffekte verhindern ebenfalls die Konvergenz dieses Verfahrens.
Bei umfangreicheren Netzwerken ergeben sich schnell Matrizen sehr hoher Dimension, die jedoch in der Regel dünn besetzt sind. Mittels geeigneter numerischer Algorithmen lassen sich diese effizient bearbeiten [4].